あるデータを分析するとき、多くの人が最初にとるステップのひとつが平均値を計算することだ。自分の身長と住んでいる地域の平均身長を比較したり、好きな野球選手の打率を自慢したりするかもしれない。しかし、平均値はデータセットの研究に役立つが、重要な限界がある。
この限界を無視した平均値の使い方は、差別や傷害、さらには命に関わる事故といった深刻な問題を引き起こしている。
例えば、アメリカ空軍はかつて「平均的な人間」を想定して飛行機を設計していたが、パイロットが飛行機をコントロールできなくなったため、そのやり方を放棄した。平均値には多くの使い道があるが、データセットのばらつきについては何も教えてくれない。
私は専門分野に特化した教育研究者であり、エンジニアリングを中心に、人がどのように学ぶかを研究している。私の研究には、エンジニアが仕事において平均値をどのように使っているかという研究も含まれている。
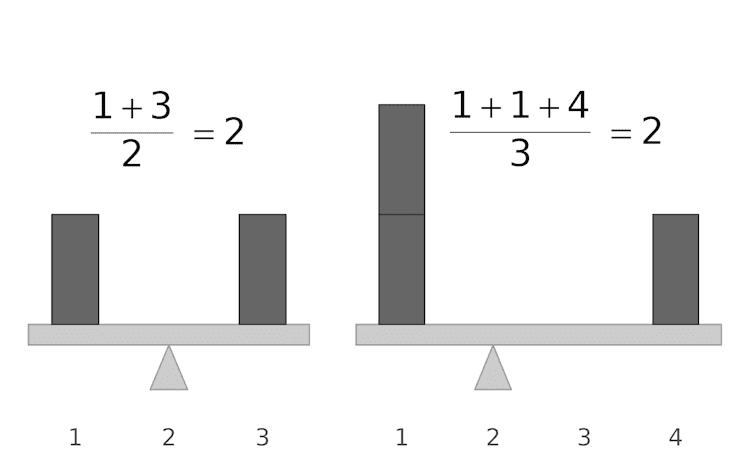
平均を使ってデータを要約する
平均の歴史は古く、紀元前9世紀か8世紀にはその使用が記録されている。初期の例では、ギリシャの詩人Homerusが平均を取ることによって船の兵士の数を推定した。
初期の天文学者は、将来の星の位置を予測したかった。しかし、こうした予測を行うには、まず星の現在位置を正確に測定する必要があった。複数の天文学者が独自に位置測定を行ったが、しばしば異なる値になった。星の真の位置は1つしかないため、この食い違いが問題となった。
1632年のGalileoは、このような測定の違いに対処するための体系的なアプローチを推し進めた最初の人物である。彼の分析が誤差論の始まりである。誤差論は、科学者が測定の不確かさを減らすのに役立つ。
誤差論と平均
誤差論では、研究者は一連の測定値を、誤差によって破損された真の値の周辺にあると解釈する。天文学では、星の位置は正確であるが、初期の天文学者は手が不安定であったり、望遠鏡の画像がぼやけていたり、天候が悪かったりした。これらはすべて誤差の原因だ。
誤差に対処するため、研究者はしばしば測定値が不偏であると仮定する。統計学では、これは中心値の周りに均等に分布することを意味する。不偏の測定値にも誤差はあるが、それらを組み合わせることで、真の値をよりよく推定することができる。
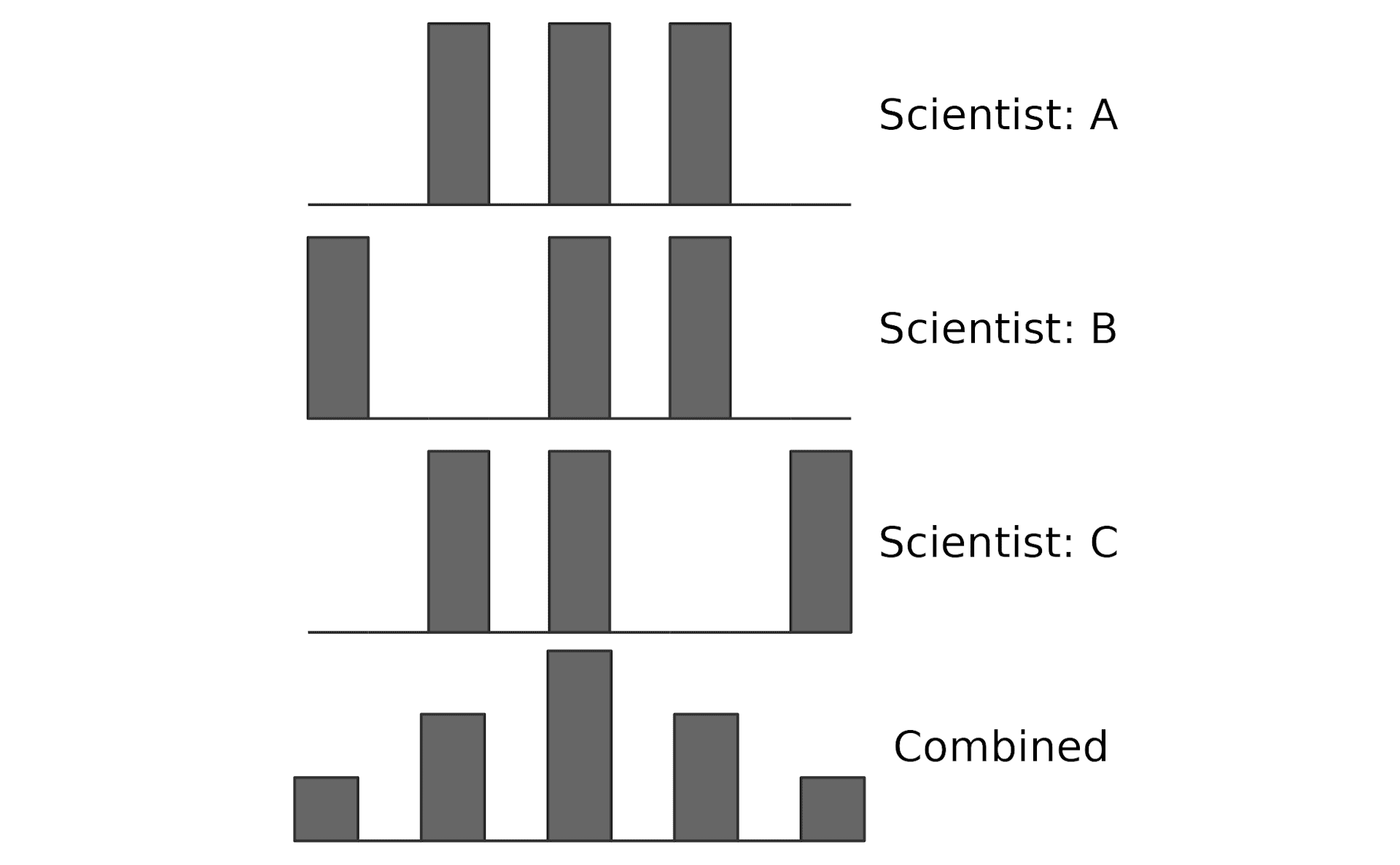
3人の科学者がそれぞれ3つの測定をしたとする。別々に見ると、彼らの測定値はランダムに見えるかもしれないが、偏りのない測定値をまとめると、平均値という真ん中の値の周りに均等に分布する。
測定値に偏りがない場合、平均値はすべての測定値の真ん中に位置する傾向がある。実際、平均値がすべての可能な測定値に最も近いことを数学的に示すことができる。この理由から、平均は測定誤差に対処するための優れたツールである。
統計的思考
誤差論は、当時は革命的だと考えられていた。他の科学者たちは天文学の正確さに感心し、同じアプローチを自分たちの分野にも取り入れようとした。19世紀の科学者Adolphe Queteletは、誤差論からのアイデアを人間の研究に応用し、人間の身長と体重の平均を取るというアイデアを導入した。
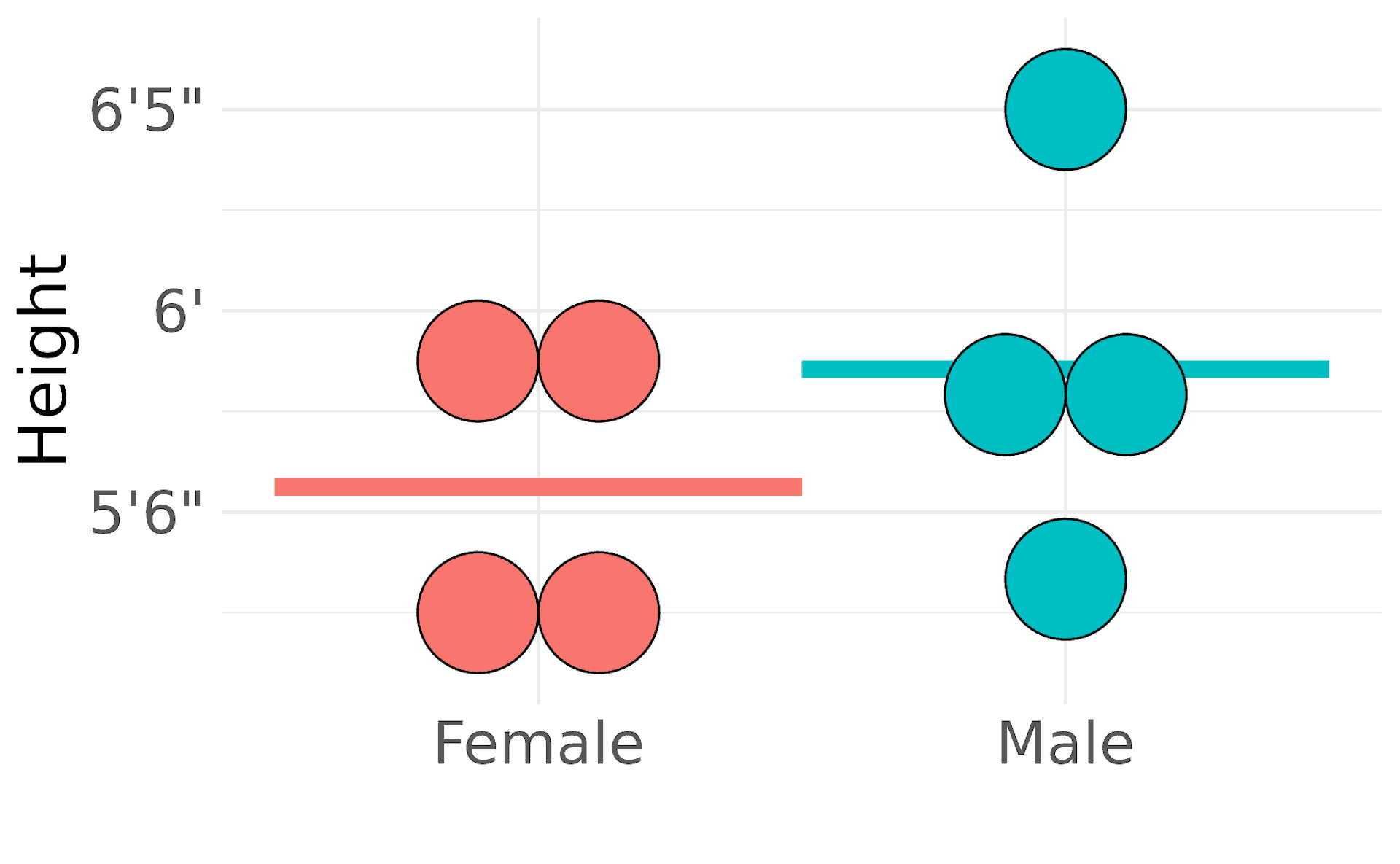
平均はグループ間の比較に役立つ。例えば、男性と女性の身長のデータセットから平均をとれば、データセットの男性は女性より平均的に背が高いことがわかる。しかし、平均値ですべてがわかるわけではない。同じデータセットの中に、男性より背の高い女性を見つけることもできるだろう。
そのため、平均値だけを考慮することはできない。統計的に考えることによって、値の広がりも考慮すべきだ。統計的思考とは、ばらつき、つまり測定値が異なる傾向について注意深く考えることと定義される。
例えば、異なる天文学者が同じ星を測定し、異なる位置を記録することは、ばらつきの一例である。天文学者たちは、そのばらつきがどこから来るのかを注意深く考えなければならなかった。恒星の真の位置は1つであるため、天文学者たちはそのばらつきが誤差によるものだと安全に考えることができた。
測定値の平均を取ることは、ばらつきが誤差に起因する場合には理にかなっている。しかし、実際にばらつきがある場合に平均値を解釈する際には、研究者は注意しなければならない。例えば、身長の例では、平均身長が男性の方が高くても、個々の女性の方が男性よりも高いことがある。平均値だけに注目すると、ばらつきが無視され、それが深刻な問題を引き起こしている。
Queteletは誤差理論から平均を計算する習慣を取り入れただけではない。彼はまた、単一の真の値を仮定した。彼は「平均的な人間」という理想を持ち上げ、人間のばらつきは基本的に誤りであり、つまり理想的なものではないと示唆したのである。Queteletに言わせれば、身長が正確な平均値でなければおかしいということになる。
社会規範を研究する研究者たちは、Queteletの「平均的な人間」についての考え方が、「普通」という言葉の現代的な意味、つまり普通の身長や普通の行動を生み出したと指摘している。
これらの考え方は、初期の統計学者など一部の人々によって、集団を2つに分けるために使われてきた。
例えば、優生学運動(「劣った」人々が子供を産むのを防ぐための卑劣な取り組み)は、「正常な」人々に関するこのような考え方に端を発している。
誤差としてのばらつきというQueteletの考え方が差別の実践を支える一方で、Queteletのような平均値の使い方は、現代の工学の失敗にも直結している。
平均値の失敗
1950年代、米国空軍は “平均的な人間 “を対象に航空機を設計した。平均的な身長、平均的な腕の長さ、その他いくつかの重要な寸法に沿って平均的に設計された飛行機は、ほとんどのパイロットにとって機能するだろうと想定していた。
この決定は、1日に17人ものパイロットが墜落する一因となった。”平均的な人間”」”であれば飛行機を完璧に操作できるが、実際のばらつきが邪魔をした。背の低いパイロットは視界が悪くなり、手足の長いパイロットは体にフィットさせるために体を縮めなければならない。
空軍は、ほとんどのパイロットがすべての主要な寸法において平均に近いと想定していたが、4,063人のパイロットのうち、平均的なパイロットはゼロであることが判明した。
空軍は、パイロットのばらつきを考慮し、調整可能なシートを設計することで問題を解決した。
調整可能なシートは今では当たり前のように思えるかもしれないが、この「平均的な人間」という考え方は今日でも問題を引き起こしている。米国では、自動車事故で重傷を負う確率は女性の方が約50%高い。
政府会計検査院は、この格差の原因を、空軍の “平均的な男性”と同じように、男性ダミーを縮小したものを使って女性の乗員を粗雑に表現している衝突試験のやり方に求めている。最初の女性衝突試験用ダミーは2022年に導入されたが、米国ではまだ採用されていない。
平均値は有用だが、限界がある。真の値の推定やグループ間の比較には、平均値が威力を発揮する。しかし、実際のばらつきを示す個人に対しては、平均はそれほど意味を持たない。







コメントを残す