数学の世界では、ユニークな性質を持つ新しい形が発見されることは、常にエキサイティングな出来事だ。3月にユニークな図形 “Einstein”が発見されたのに続き、“Spectre”と名付けられた別の図形が、その優れた特性で話題を呼んでいる。

Spectre：非周期的タイリングの新境地

今年初め、コンピュータ科学者のチームが、1つの形状だけで平らな表面を完全に覆うことができるユニークな形状、”Einstein”または “the hat”を発見した。特定のパターンを繰り返すことなく表面を覆うこのユニークなパターンは「非周期的タイリング」と呼ばれ、長年にわたり数学分野の課題となっていた。

非周期タイリングを発見する旅は、1960年代に数学者Hao Wangが「平面を繰り返しなくタイリングできる図形の集合を見つけることは不可能である」という仮説を立てたことから始まった。しかし、この仮説は、Wang氏の弟子であるRobert Berger氏によって否定され、2万個以上のタイルの集合が発見された。その後、数理物理学者のRoger Penrose氏によって2セットまで減らされ、今年ついに1つの形状で非周期的タイリングを実現する”Einstein”が発見されるに至った。

しかし、この”Einstein”には、表面のある部分を覆うために鏡像が必要であるという注意点があり、このプロセスには厳密には2つの異なる形状が含まれているという意見もあった。そこで、鏡像を必要とせず、非周期的なタイリングが可能な新しい形状を探し求めることになった。

その結果、”Einstein”に近い形状である“Spectre（怪物）”が発見されたのだ。”Einstein”の「正三角形バージョン」に手を加えて発見された“Spectre”は、鏡像を必要とせずに非周期タイリングを行う能力を示したのだ。この発見の共著者でイギリス・ケンブリッジのソフトウェア開発者であるJoseph Myers氏は、「このようなタイルが存在することに驚きはありませんでした。ただし、“Einstein”と密接に関係するものが存在したことは驚きでした」と、彼は述べている。

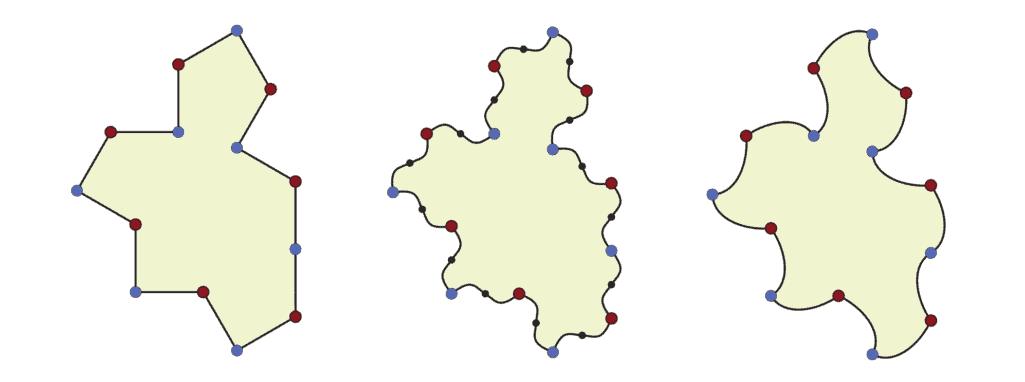
この発見は、数学におけるタイリングの研究に大きな一歩を踏み出すものと考えられ、その影響は学問の枠を超えて広がっている。この“Spectre”形状は、サッカーボールやシャワーカーテンの革新的なデザインなど、興味深い応用につながる可能性があり、数学の発見が日常生活といかに交わるかを示している。この成果は、オックスフォード大学で開催される特別イベントで祝される予定だ。

厳密にキラルな非周期的モノタイルである「Spectre」は、非周期的タイリングの世界においてゲームチェンジャーであることが証明されている。一つの図形が並進と回転だけで非周期的なタイリングができることを証明したことで、この魅力的な数学の分野の探求と応用に新しい可能性をもたらすだろう。

論文

• arXiv: A chiral aperiodic monotile

参考文献

• University of Waterloo: A chiral aperiodic monotile
• The Aperiodical: Now that’s what I call an aperiodic monotile!

研究の要旨

最近発見された「The Hat」の非周期的なモノタイルは、反射しないタイルと反射するタイルが混在しており、一つの形が並進と回転だけで非周期的なタイルを作ることができるかという疑問が残されている。我々は、The Hatの近縁種である正三角形が弱キラルな非周期的モノタイルであることを示し、反射を禁止した場合、非周期的なティリングしか認めないことを示す。さらに、この多角形の辺を修正することで、Spectresと呼ばれる、厳密にキラルな非周期的モノタイルである形状のファミリーを得ることができる。