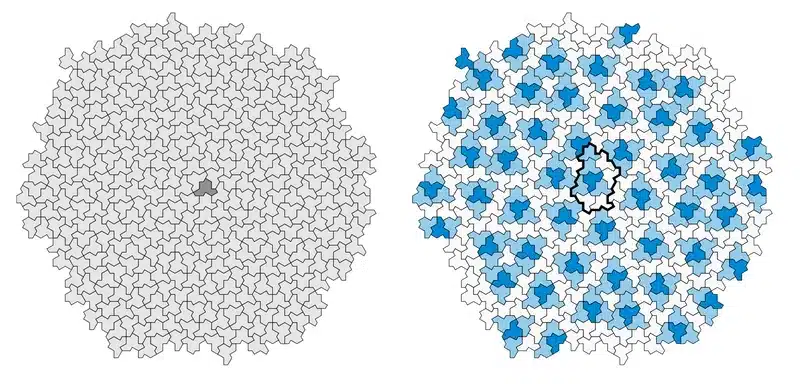
コンピュータ科学者たちは、何十年もかけてようやく「Einstein」と名づけた新しいタイルを発見した。それは、13の側面を持つ1つの形状で、一度も同じパターンを繰り返すことなく平面全体を覆うことが出来るものだ。
数学の世界では「非周期的モノタイル」と呼ばれるこのタイプの形状は、物質科学の分野で実際に応用されている形状である。数学者たちは、この発見を非周期タイルの歴史におけるブレークスルーと称えている。
このタイルは「Einstein」と呼ばれているが、有名な物理学者にちなんだ名前ではない。ドイツ語で「1つの石」を意味するein steinからきており、1枚のタイルであることを意味している。研究者らは、この研究成果をプレプリントサーバーarXivに掲載した論文で発表した。
「この論文で、我々は、最初の真の非周期的なモノタイル、すなわち、幾何学のみによって非周期性を強制し、マッチング条件によって追加の制約を適用しない形状を提示する我々は、この形状、我々が『帽子』と呼ぶポリカイトが、置換システムに基づいてタイリングに組み合わされなければならないことを証明します」と、ウォータールー大学のコンピュータ科学教授で論文の4人の著者の一人であるCraig Kaplan氏は述べている。
Kaplan氏はTwitterのスレッドで、最初の非周期的な集合は20,000以上のタイルで構成されていたと付け加えている。「その後の研究により、その数は減り、92個、6個、そして1974年に考案された有名なペンローズ・タイルという形を経て2個になった」と、その歴史を振り返る。
それ以来、Kaplan氏は「他の人たちが2サイズのセットを作ったが、誰も平面を非周期的にタイル状にする単一の形状である『Einstein』を見つけることができなかった」と説明した。「果たしてそんな形が存在するのでしょうか?」
そして今回、コンピュータ科学者の国際チームが、信じられないことに、このユニークな形状を発見することが出来たのだ。新しい論文では、コンピュータ・モデリングによってこの形状の性質をどのように証明したかが説明されている。基本的には、Einsteinタイルは、繰り返しパターンを示すことなく、表面を完全に覆うことができることを示したのだ。
この論文はまだ査読を受けていないが、専門家たちは、この論文が精査に耐える可能性が高いと信じている。このタイルを発見し、その非周期性を証明するには、強力なコンピューターと人間の創造性の両方が必要だったと、Chaim Goodman-Strauss氏は『New Scientist』のインタビューで語った「文字通り、100万分の1のものを探しているのです。999,999のつまらないものを除外して、奇妙なものを見つけ、それをさらに探求する価値があるのです」
「そして、手で調べて理解しようとし、構造を引き出し始めます。人間が理解できる証明を構築するためには、人間が関与しなければならないので、コンピュータの意味がないのです」と、彼は付け加えた。
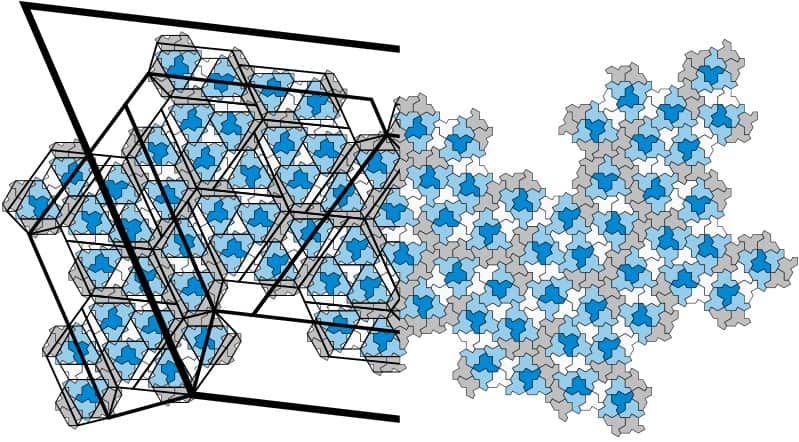
その証明は、最も基本的な形で、2つのステップから構成されている。まず、「帽子」が特別なものであることを示すヒントとして、「帽子」がより大きなクラスター、すなわち「メタタイル」に配列する傾向があることが挙げられる。これは非周期的なタイリングによく見られる現象で、この形がEinsteinである可能性を示す大きな手がかりとなった。
しかし、その非周期性を証明するためには、少し違った手法が必要だった。そこで研究チームは、帽子を引き伸ばしたり変形させたりして、同じ繰り返しパターンを持つが、2つの極端な形状の間のさまざまな段階にあるタイルのファミリーを連続的に作成した。このような極端な状態を考慮することで、帽子が作り出すタイルが確かに非周期的であることを示すことができたのだ。
この新しい形は幾何学者を興奮させるかもしれないが、真の非周期的モノタイルを発見したことの意味は、地元の大学の純粋数学科の枠を超えたところにある。準結晶は、クリネックスからターミネーター型ロボットまで、あらゆるものに応用されているのだ。
論文
- arXiv: An aperiodic monotile
参考文献
- University of Waterloo: An aperiodic monotile
- via New Scientist: Mathematicians discover shape that can tile a wall and never repeat
研究の要旨
「アインシュタイン」とも呼ばれる非周期的なモノタイルは、平面のティリングを許容するが、周期的なティリングは決して許容しない形状であり、長年の未解決問題である。我々は、トポロジカルディスクタイルについて、組み合わせ論的に等価な非周期的多角形の連続性を示すことで、この問題に答える。まず、代表的な例である「帽子」多角形が「メタタイル」と呼ばれるクラスターを形成することを示し、それに対して置換規則を定義することができる。メタタイルは平面のタイリングを認めるので、帽子も同様である。次に、新しい幾何学的非整合性論証により、多角形の連続体の一般的なメンバーが非周期的であることを証明する。これとは別に、帽子が階層的な–つまり非周期的な–タイリングを形成しなければならないことを、組み合わせ論的、コンピュータ支援的に証明する。







コメントを残す